Homomorfismo evaluación — Sean dos anillos y de forma que R es subanillo de S. Sea . Construimos la aplicación que a cada polinomio le hace corresponder su evaluación en α, i.e., β(p) = p(α). E … Wikipedia Español
Extensión de cuerpo — Saltar a navegación, búsqueda En Álgebra, las extensiones de cuerpo son el problema fundamental de la Teoría de Cuerpos. Un cuerpo es un conjunto en el que las operaciones suma y producto están definidas y funcionan bien . Cuando se construye una … Wikipedia Español
Elemento algebraico — Saltar a navegación, búsqueda Un elemento algebraico sobre un cierto cuerpo matemático es un elmento de un conjunto que contiene a dicho cuerpo matemático y que constructible a partir de ciertas operaciones algebraicas relacionadas con los… … Wikipedia Español
Álgebra asociativa — En matemáticas, un álgebra asociativa es un módulo que también permite la multiplicación de vectores de manera distributiva y asociativa. Contenido 1 Definición general 2 Caso especial en el que el anillo es un cuerpo 2.1 Ejemplos … Wikipedia Español
Elemento trascendente — Saltar a navegación, búsqueda La Teoría de Cuerpos es una rama de la Teoría de Anillos, que a su vez es una rama del Álgebra Abstracta. Uno de las principales campos de estudio de la Teoría de Cuerpos es el de decidir si un polinomio cuyos… … Wikipedia Español
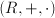 y
y 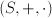 de forma que
de forma que 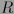 es subanillo de
es subanillo de 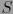 . Sea
. Sea 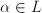 .
Construimos la aplicación
.
Construimos la aplicación 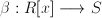 que a cada polinomio
que a cada polinomio 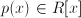 le hace corresponder su evaluación en
le hace corresponder su evaluación en 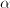 , i.e.,
, i.e., 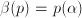 . Esta aplicación es un isomorfismo de anillos (que se denomina homomorfismo evaluación):
●
. Esta aplicación es un isomorfismo de anillos (que se denomina homomorfismo evaluación):
● 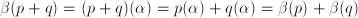 ;
●
;
● 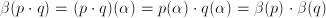 ;
cualesquiera que sean
;
cualesquiera que sean 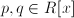 .
Además, si R y S fuesen anillos y unitarios entonces:
●
.
Además, si R y S fuesen anillos y unitarios entonces:
● 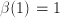 ,
,